2.1 'Inercia y la primera ley de Newton'
La primera ley de Newton nos expresa: "Que un objeto permanece en reposo si actua sobre el una fuerza resultante = 0"
Si la fuerza resultante que actua sobre un objeto en movimiento es cero, el objeto continuara su movimiento con velocidad constante.
Si la suma vectorial de las fuerzas esternas que actuan sobre un objeto es cero, la velocidad del objeto permanecera constante.
La inercia mide la tendencia de un objeto en reposo a permanecer en reposo y de un objeto en movimiento a permanecer en movimiento con su velocidad original.
2.2 Accion y Reaccion (tercera ley de Newton)
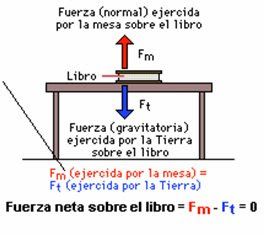
La tercera ley , también conocida como Principio de acción y reacción nos dice que si un cuerpo A ejerce una acción sobre otro cuerpo B, éste realiza sobre A otra acción igual y de sentido contrario .
Esto es algo que podemos comprobar a diario en numerosas ocasiones. Por ejemplo, cuando queremos dar un salto hacia arriba, empujamos el suelo para impulsarnos. La reacción del suelo es la que nos hace saltar hacia arriba.
Cuando estamos en una piscina y empujamos a alguien, nosotros también nos movemos en sentido contrario. Esto se debe a la reacción que la otra persona hace sobre nosotros, aunque no haga el intento de empujarnos a nosotros .
2.3 Segunda ley de Newton.
La masa y la inercia de un objeto afectan su aceleración bajo la acció de una fuerza dada , cuando mayor sea la inercia de un objeto , sera mas dificil que pueda acelerarce ; las fuerzas de friccion interactuan en los procesos de aceleración de los objetos.
La Segunda ley de Newton se encarga de cuantificar el concepto de fuerza. Nos dice que la fuerza neta aplicada sobre un cuerpo es proporcional a la aceleración que adquiere dicho cuerpo . La constante de proporcionalidad es la masa del cuerpo , de manera que podemos expresar la relación de la siguiente manera :
F=ma
Tanto la fuerza como la aceleración son magnitudes vectoriales, es decir, tienen, además de un valor, una dirección y un sentido. De esta manera, la Segunda ley de Newton debe expresarse como:
F = m a
La unidad de fuerza en el Sistema Internacional es el Newton y se representa por N . Un Newton es la fuerza que hay que ejercer sobre un cuerpo de un kilogramo de masa para que adquiera una aceleración de 1 m/s2 , o sea,
1 N = 1 Kg · 1 m/s2
La masa y la inercia de un objeto afectan su aceleracion bajo la accion de una fuerza dada, cuanto mayor sea la inercia de un objeto sera mas dificil que pueda acelerarse, las fuerzas de friccion interaccionan en los procesos de aceleracion de los objetos.
2.4 Masa y peso
¿ Que tenemos que saber antes de aplicar la leyes de Newton?
Masa Peso
: :
: :
Cantidad de materia Interacción de la masa con la gravedad.
que tiene un cuerpo.
Masa peso
: :
: :
: :
: :
: ....... Densidad......... :
:
:
:
Cantidad de materia.......:.......A mayor densidad, mayor gravedad.:
contenida en un volumen.

Cuando se habla de masas en movimiento ,a la interacción de la masa con la velocidad le llamamos inercia, el peso de un objeto se expresa de acuerdo con la siguiente relación:
Unidad estandar de la masa en el S.I (m,k,s) es el kilogramo.
W= m * g donde : m= masa.
W= peso (Weight). g= gravedad.
*Notacion vectorial.
Fuerza= masa x aceleración.
P + w= fuerza de cuerpo.
P presión
rescribimos como
P + W = m a
2.5 Aplicación de la segunda ley de Newton
P= presión.
Se expresa como:
P = P j
W¨= peso
Se expresa: w = -w j
Tenemos entonces:
( P - W) J = m a
Si el empuje de la masa P es igual al empuje del libro W, el libro no se acelera, permanece en reposo.
Si se considera un objeto que se encuentra colocado en un sistema de 3 dimensiones, y si se considera una multiplicidad de fuerzas, entonces el plano de referencia aumenta su complejidad.

F₁ + F₂ + F ₃+……F n=ma
:
:
:
Un objeto sujeto a N cantidad de fuerza.
Agrupando fuerzas en X,Y, Z.
Tenemos: ( F₁x+F₂x+F₃x…..Fnx) i+ (F₁y+F₂y+F₃y……. Fny) J +(F₁z+F₂z+F₃z……..Fnz)k =m (a xi+ayi+azk)
2.6 Fuerzas de friccion
Fuerza de fricción viscosa (cuando los objetos se mueven a través de gases o líquidos).
Fuerzas de friccion del aire que actuan sobre un automovil.
Fuerzas de fricción en rodamiento (cuando un objeto rueda en una superficie plana).
(En la zona del piso y la llanta ocurre una deformación para ambos)
Fuerzas de fricción de desplazamiento (dos superficies en contacto ejercen una sobre la otra para oponerse al desplazamiento).
Coeficientes de fricción estático y dinámico.
Un coeficiente de fricción estático trabaja en un sistema donde la aceleración es igual con O, es que no existe movimiento, en tanto que el coeficiente de fricción cinético o dinámico actúa sobre un objeto en movimiento.
Las ecuaciones que describen estos 2 coeficientes de friccionan expresan como:
Fuerza de fricción estática. Fuerza de fricción dinámica.
ƒc =µs* FN ƒk = µk * FN
Donde :
ƒc = Coeficiente de fricción coeficiente Estático.
ƒk = Coeficiente de fricción dinamico
FN = Fuerza normal a la superficie
• Coeficientes de fricción.
Material µc µk
Huele sobre Concreto ~ 0.4 ~ 0.7
Madera sobre Nieve 0.08 0.06
Acero sobre teflón 0.08 0.04
Acero sobre acero 0.75 0.75
Madera sobre Madera 0.7 0.4
Metal Metal lubricado 0.10 0.07
Vidrio sobre Vidrio 0.9 0.4
2.7 Relacion de conceptos
Interacción de fuerzas normales (FN).
CASO 1
Fn=W₁
CASO 2
Fn=W₁ + W₂
CASO 3
Fn=W₁ - Fsenѳ
Problema:
Una masa de 7 kg. Esta sujeta a las fuerzas mostradas ¿Encontrar su aceleracion?
∑ Fx = max= (80cos22º-50sen30º) N= (7.0Kg)ax
= (40(0.9771) -50(0.5)) N= 7.0Kg ax
= (40(0.9771) -50(0.5)) N= 7.0Kg ax
= (37.03 - 25) N= 7.0Kg ax
= 12.08 N= 7.0 Kg ax
∑ Fy=may= (40sen22º + 50cos30º) N= (7.0Kg) ay
=58.8 N= (7.0Kg)ay
F=(masa)(aceleración)
El despeje se expresa como:
Aceleración = Fuerza/Masa
ax = 12.08 N / 7 kg = 1.725N/kg ay = 58.8 N / 7 kg = 8.4 N / kg
Para hallar la aceleración resultante trabajamos con el teorema de Pitágoras.
a=√ax²+ay²
a=√(1.725ⁿ/10a)²+(8.4ⁿ/Kg)²
a=√73.63 N²/Kg
a=8.57N/kg
El ángulo se encuentra de la siguiente manera:
tg ̄¹ =8.4 N/kg ÷ 1.725 N/kg
tg ̄¹=8.86
ѳ=78.3